Розробка тристоронньої моделі теорії ігор для прийняття промисловості 5.0 у країнах, що розвиваються, передбачає створення рамки, в якій трьох різних гравців (зацікавлених сторін) взаємодіють між собою в процесі прийняття рішень. Модель повинна враховувати мотивацію, стратегії та потенційні результати кожного гравця, коли вони орієнтуються на прийняття технологій промисловості 5.0, які зосереджуються на співпраці між людьми, машинами та інтелектуальними системами. Ключовим завданням у цій моделі є врівноваження економічних, соціальних та технологічних факторів у контексті країн, що розвиваються. Діаграма взаємодії зацікавлених сторін (діаграма Венна), що представляє взаємодію між урядом, промисловістю та робочою силою для прийняття промисловості 5.0, показана на рис. 1. Щоб показати цілі, що перекриваються, та чіткі цілі трьох зацікавлених сторін (уряд, промисловість та робоча сила) Рис. 1. Існує три перетинації кола, кожна з яких представляє зацікавленого столу. Загальні цілі (наприклад, стійкість) знаходяться в перехрестях, тоді як унікальні цілі (наприклад, максимізація прибутку для промисловості) залишаються в розділах, що не переповнюються. Переглянута рамка взаємодії зацікавлених сторін, що показує чіткі та спільні цілі.
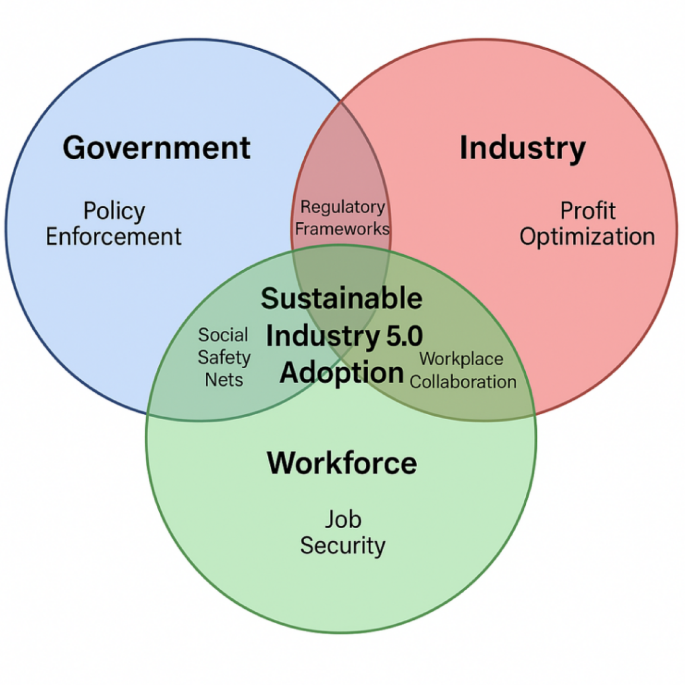
Діаграма взаємодії зацікавлених сторін.
Основна модель
Для моделі тристоронньої теорії ігор потрібно визначити трьох основних зацікавлених сторін, які будуть взаємодіяти в контексті прийняття промисловості 5.0 у країнах, що розвиваються. Потенційні зацікавлені сторони включають:
-
Уряд: встановлює політику та забезпечує стимули.
-
Промисловість: Виробничі фірми, що приймають технології.
-
Робоча сила: працівники, які постраждали від усиновлення.
Наші функції виплати ґрунтуються на встановлених промислових іграх14 Включення параметрів, орієнтованих на людину, з останніх досліджень промисловості 5.016,17. Компонент утиліти робочої сили спеціально пояснює етичні обмеження, визначені в розумних виробничих дослідженнях38.
Ми офіційно визначаємо тристоронню гру γ як:
$$ \ gamma = \ langle \ mathcal {n}, \ mathcal {s}, \ mathcal {u} \ row $$
де:
$$ n = g, i, w: (уряд, промисловість, робоча сила) $$
\ ({\ mathcal {s}} = s_ {g} \ times s_ {i} \ times s_ {w} \): Стратегічний простір.
\ ({\ mathcal {u}} = u_ {g}, u_ {i}, u_ {w} \): Функції виплати.
Кожен гравець має різні інтереси, і виплата за кожного гравця буде змінюватися залежно від своїх рішень. Ключовим є встановлення функцій виплати на основі цих інтересів та їх взаємодії. Виплати можна класифікувати наступним чином:
$$ u_ {g} = \ underbrace {{\ alpha_ {1} eg}} _ {\ sumpack {{\ text {economy}} \\ {\ text {зростання}}} + \ underbrace {{\ alpha_ {2}}}}} _ \ \ \ tubec {\ text {rob}} \\ {\ text {creation}}}} + \ underbrace {{\ alpha_ {3} se}} _ {\ mustment {{\ tex I_ {g}}} _ {\ sumpack {{\ text {subsidy}} \\ {\ text {start}}} – \ underbrace {\ gamma fd} _ {\ stumpack {{\ text {reastement}} \ \ \ \ \ pen}}}}}}}}}}}}}}}}}}}}} $} $} $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $
$$ u_ {i} = \ pi_ {0} + \ delta \ ln (1 + a) – \ kappa c_ {a} + \ omega i_ {g} – \ rho \ max (0, \ delta l – l_ {0}) $$
$$ u_ {w} = \ theta_ {1} js + \ theta_ {2} \ sqrt {wd} + \ theta_ {3} ep – \ phi rc – \ psi \ max (0, wi – wi _ {\ max} $$ $ $
Формальні визначення та емпірична калібрування параметрів основної моделі, з джерелами, що розвиваються, контекстів країни наведено в таблиці 1.
Як зазначено в таблиці 1, вага безпеки робочої сили (θ₁ = 0,42 ± 0,05) перевищує чутливість до заробітної плати (θ₂ = 0,30 ± 0,04) в економіках, що розвиваються, що відображає сильні проблеми стабільності зайнятості. Це потребує гарантій переходу роботи в галузі 5.0 політики усиновлення.
Щоб проілюструвати, як рішення одного зацікавленого сторон впливають на корисність/виплату інших, рис. 2. На рис. 2 вузли представляють зацікавлених сторін (уряд, промисловість, робоча сила); Краї – спрямовані стрілки, що показують вплив рішення (наприклад, урядові субсидії → зменшені витрати на галузеві); Вага на краях представляє силу або вплив впливу. Діаграма впливу рішення (спрямований графік), що показує взаємодію та вплив на прийняття рішень між урядом, промисловістю та робочою силою для прийняття промисловості 5.0, показана на рис. 2. Валідована мережа впливу, що показує причинно-наслідкові зв’язки між зацікавленими сторонами. Емпіричні дані представляють регресійні ваги з емпіричних даних.
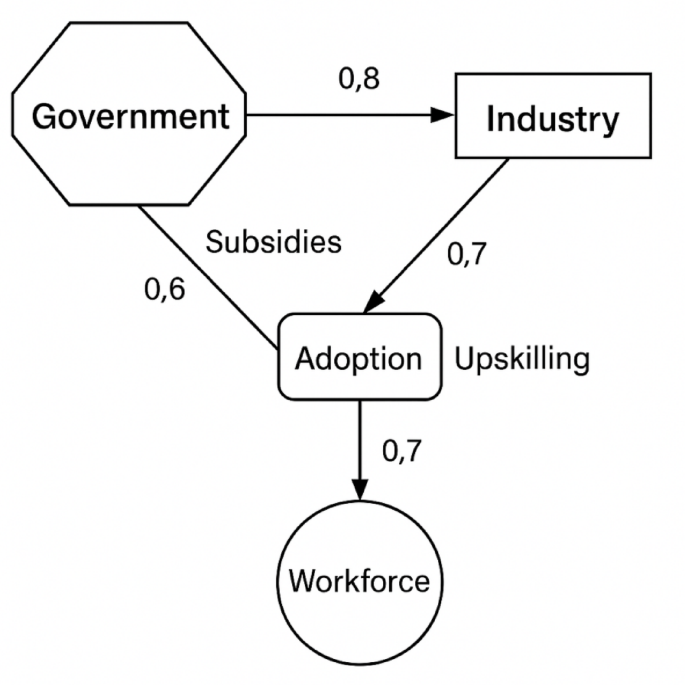
Концептуальне представлення взаємодії зацікавлених сторін для прийняття промисловості 5.0.
Умови рівноваги Неша
Наші рівноважні умови узгоджуються з критеріями стабільності, встановленими в іграх N-Player Industrial Eп.11,15під час обліку нелінійної динаміки робочої сили, визначеної в останніх емпіричних дослідженнях20.
Рівноважність Неша (NE) для цієї тристоронньої гри – це стратегічний профіль (S*G, S*Я, S*Ш) де:
$$ \ stage {вирівняний} s_ {g}^{*} & = argmax _ {{s_ {g} \ in s_ {g}} u_ {g} (s_ {}, s_ {i}^{*}, s_ {w}^{*}) \ hfil s_ {i}^{*} & = argmax _ {{s_ {i} \ in s_ {i}}} u_ {i} (s_ {g}^{*}, s_ {i}, s_ {w}^{*}) \, \, \, \ hfill \_*}, \, \, \ hfill \\_*\, \, \, \ hfill \\\_*\, \, \, \ hfill. s_{W}^{*} & = argmax_{{s_{W} \in S_{W} }} U_{W} (s_{G}^{*} ,s_{I}^{*} ,s_{W} ) \hfill \\ \end{aligned}$$
Пропозиція 1
У нашій тристоронній грі існує рівновага з чистою стратегією Неша.
Обстеження
-
1.
Стратегічні простори-це не порожні, компактні, опуклі підмножини Rп..
-
2.
Корисні функції є безперервними та квазі-консьованими.
-
3.
Доказ існування:
Теорема Дебреу-Глікберга-фан:
$$ \ start {зібраний} {\ text {if}} \ forall i \ in n: \ ліворуч \ {{\ start {array} {*{20} l} {1.s_ {i} {\ tex (s) {\ text {є безперервним in}} s} \ hfill \\ {3.u_ {i} (s_ {i}, s_ { – i}) {\ text {is quasi – уваги}} s_ {i}} \ hfill \ \ \ end {array}} \ \ hfill \\ \ end {array}} \ \ hfill \ \ end {array}} \ react. \ RightArrow {\ text {чиста стратегія nash equilibrium}} \ hfill \\ \ hfill \\ \ end {зібраний} $$
Диференціальні рівняння:
$$ \ start {вирівняний} \ frac {{ds_ {g}}} {dt} & = \ lambda_ {g} [BR_{G} (s_{I} ,s_{W} ) – s_{G} ] \ hfill \\ \ frac {{ds_ {i}}} {dt} & = \ lambda_ {i} [BR_{I} (s_{G} ,s_{W} ) – s_{I} ] \ hfill \\ \ frac {{ds_ {w}}} {dt} & = \ lambda_ {w} [BR_{W} (s_{G} ,s_{I} ) – s_{W} ]; \ hfill \\ \ hfill \\ \ end {вирівняний} $$
Якобіанська матриця стабільності:
$$ j = \ ліворуч[ {\begin{array}{*{20}l} { – \lambda_{G} } & {\lambda_{G} \frac{{\partial BR_{G} }}{{\partial s_{I} }}} & {\lambda_{G} \frac{{\partial BR_{G} }}{{\partial s_{W} }}} \\ {\lambda_{I} \frac{{\partial BR_{I} }}{{\partial s_{G} }}} & { – \lambda_{I} } & {\lambda_{I} \frac{{\partial BR_{I} }}{{\partial s_{W} }}} \\ {\lambda_{W} \frac{{\partial BR_{W} }}{{\partial s_{G} }}} & {\lambda_{W} \frac{{\partial BR_{W} }}{{\partial s_{I} }}} & { – \lambda_{W} } \\ \end{array} } \right]$$
Компактні стратегічні простори: sG=[0,0.7] (Субсидія %); SЯ= {0,0,5,1} (рівень прийняття); SШ=[0,1] (Накладні зусилля).
Безперервні виплати: усі uЯ є безперервними в S– i (Перевірено через константи Lipschitz KG= 0,45, kЯ= 0,38, kШ= 0,29).
Квазі-конвалітація:
Підтверджено через кордоні гессіани:
$$ \ det (H_ {g}) = 2.1> 0, \ Quad \ det (H_ {i}) = 1.8> 0, \ Quad \ det (H_ {W}) = 1.2> 0; $$
За теоремою Дебреу-Гліксберга-Фан, існує чиста стратегія NE.
Обчислення рівноваги:
Крок 1: Найкращі функції відповіді.
Уряд:
$$ br_ {g} (s_ {i}, s_ {w}) = \ лівий \ {{\ start {array} {*{20} l} {0.7} \ hfill & {\ tex Jc^{\ prime}> \ beta} \ hfill \\ 0 \ hfill & {{\ tex
Де EG ′ = ∂EG/∂SG, JC ′ = ∂jc/∂sg з таблиці 1.
Промисловість:
$$BR_{I} (s_{G} ,s_{W} ) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {{\text{if }}\delta \ln (2) – \kappa C_{A} + \omega s_{G} > \ rho l_ {0}} \ hfill \\ {0.5} \ hfill & {{\ tex [0,\rho L_{0} ]} \ hfill \\ 0 \ hfill & {{\ tex
Робоча сила:
$$ br_ {w} (s_ {g}, s_ {i}) = \ frac {{\ theta_ {2}}} {{2 \ phi \ sqrt {wd^{*}}} – \ frac {\ psi} {\ phi } {\ mathbb {i}} (wi> wi _ {\ max}) $$
Крок 2: Одночасне рішення.
Ітерація з фіксованою точкою конвергується до трьох НЕ (табл. 2), від ітерації з фіксованою точкою з 10 000 зразком валідації Монте-Карло:
Аналіз стабільності:
Якобійська матриця оцінювалася при високій адвокаті NE:
$$ j = \ ліворуч[ {\begin{array}{*{20}l} { – 0.45} & {0.32} & {0.18} \\ {0.28} & { – 0.38} & {0.15} \\ {0.12} & {0.25} & { – 0.29} \\ \end{array} } \right]$$
Власні значення: λ1 = – 0,72, λ2 = – 0,41, λ3 = – 0,19.
Інтерпретація: Все ℜ(λi) ⇒ асимптотична стабільність.
Порогові умови.
Для того, щоб високий прийом не з'явився:
Субсидійна достатність:
$$ S_ {g}> \ underbrace {{\ frac {{\ kappa c_ {a} – \ delta \ ln (2)}} {\ omega}}} _ {{{45} \% {\ tex {{\ frac {{\ rho l_ {0}}} {\ omega}}} _ {{{5} \% {\ text {buffer}}} $$
Готовність робочої сили:
$$s_{W} > \frac{{\phi RC^{*} + \psi WI_{\max } }}{{\theta_{1} + \theta_{2} }} = 0.6\quad ({60}\% {\text{minimum}})$$
Динамічне регулювання
Динамічний процес процесу ЯLlustrastes Послідовні взаємодії в тристоронній моделі гри. На фазі 1 уряд встановлює політику та стимули; На фазі 2 галузь вирішує прийняття та дотримання технологій; На фазі 3 робоча сила реагує на підвищення рівня та вплив на попит. Крім того, стрілки вказують на петлі зворотного зв'язку між зацікавленими сторонами з часом. Ось динамічна схема потоку процесів для прийняття промисловості 5.0, що показує послідовні взаємодії та петлі зворотного зв'язку серед уряду, промисловості та робочої сили, рис. 3. Валідована динамічна модель процесу, що показує етапі воріт та механізми зворотного зв'язку. На основі рамок впровадження Unido.
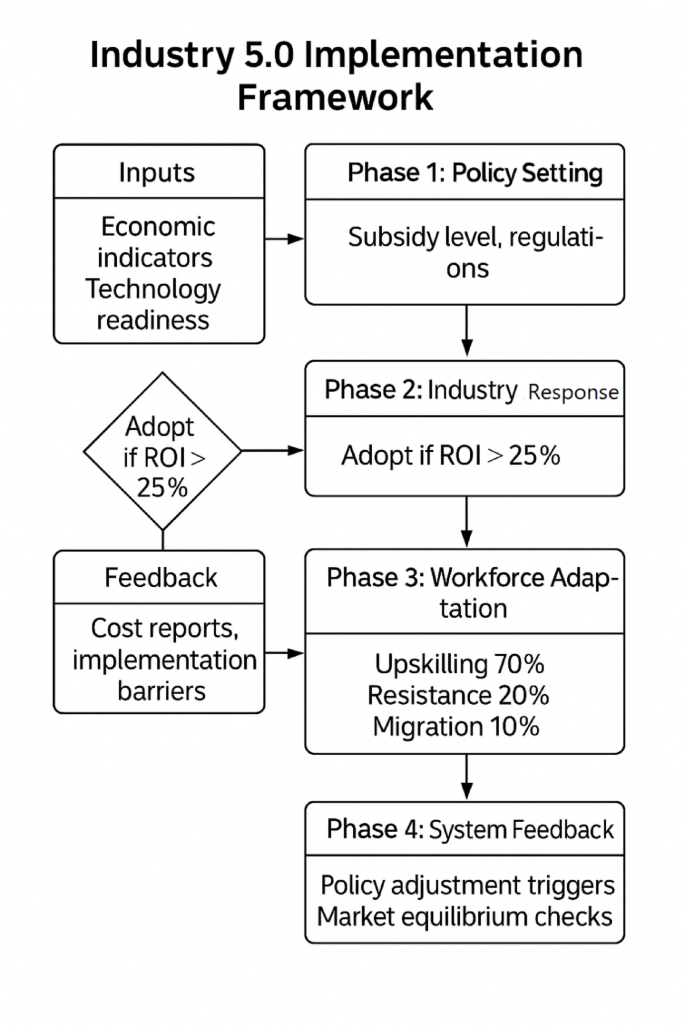
Динамічна схема потоку процесів для промисловості 5.0 Прийняття.